New Preprint Available: Geometry aware inference of steady state PDEs using Equivariant Neural Fields representations

Geometry aware inference of steady state PDEs using Equivariant Neural Fields representations (2025)

Arxiv Preprint, Under Review

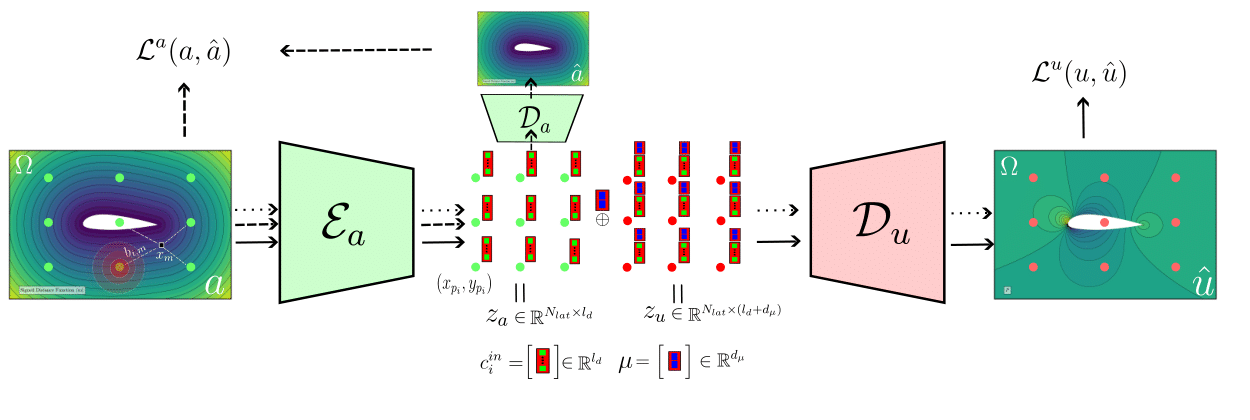
Abstract: Recent advances in Neural Fields have enabled powerful, discretization-invariant methods for learning neural operators that approximate solutions of Partial Differential Equations (PDEs) on general geometries. Building on these developments, we introduce enf2enf, an encoder–decoder methodology for predicting steady-state Partial Differential Equations with non-parameterized geometric variability, based on recently proposed Equivariant Neural Field architectures. In enf2enf, input geometries are encoded into latent point cloud embeddings that inherently preserve geometric grounding and capture local phenomena……. [shortened for brevity]